Creating REMs and Detrended DEMS with Python
Relative elevation models (REMs) adjust a DEM so that the elevation is relative to another feature instead of sea level. One common way to create a REM is to make elevation relative to a river bed.
Then, the resulting REM displays the height of each pixel above the nearest river location.
River REMs produce some wonderful, vibrant maps and visualizations of rivers. They also aid in flood analysis and geomorphic analysis by making it easier to identify important valley-bottom features.
I’ve already created a tutorial about how to create REMs in QGIS. This tutorial will demonstrate how to automate the process with Python. Most of the code is from a notebook by DahnJ. I’ve added substantial commentary and omitted a few steps.
There’s good information out there on how to create relative elevation models, but there’s usually not much explanation on why to create them (except that they look cool) and the implications for some of the creation options that are made.
Enjoy!
1. Import packages¶
There are a number of packages we’ll need to create and dispaly the REM we create. Let’s go through them quickly.
numpy: for array creation, management, and manipulationxarray: also for arraysxrspatial: the spatial version ofxarray. We’re going to use this for thehillshadeto make a visualization of our final product (Note: if you’re installing from conda-forge you’ll install the packagexarray-spatial)rioxarray: to load a raster as an xarrayshapely: for geometry manangementscipy: to create KDTree that indexes points for faster neighborhood operationsosmnx: to get river geometry from Open Street Mapmatplotlib: for plotting and visualizationdatashader: for visualization.
Now, write the code to import the require modules and functions from each package, as shown in the code below.
import numpy as np
import xarray as xr
import xrspatial
# import rasterio as rio
import rioxarray
from shapely.geometry import box
from scipy.spatial import cKDTree as KDTree
import osmnx as ox
import matplotlib.pyplot as plt
import datashader.transfer_functions as tf
2. Load a DEM¶
To start, use rioxarray to load a digital elevation model. Make sure the DEM has coverage for your river channel of interest. You’ll also want to be sure the DEM resolution is sufficient to represent the river channel in detail.
One-meter resolution should be adequte for most medium-sized rivers and 10-m resolution is adequate for many larger rivers.
I’m using a 1-meter DEM of the Snake River below Jackson Lake and in/near Grand Teton National Park (in Wyoming, United States). Fpr locations in the United States lidar-derived DEMs are available fromt the USGS Lidar Explorer (that’s where I obtained the data I’m using here).
Now load the DEM.
dem = rioxarray.open_rasterio('../data/USGS_one_meter_x52y485_WY_GrandTetonElkRefuge_2014.tif')
3. Get river geometry¶
Now, we need to relate the location of the river channel its elevation. For this we need the river’s geometry. There are multiple ways to get river geometry.
The most accurate method is to digitize the river channel directly from the DEM. I deomstrate how to do that in this article.
But since this post is all about Python, we’ll use a less-acurate method that doesn’t require any additional digitizing. We’ll pull in the river feature from Open Street Map. Here I’m able to reference the Snake River by name. You may or may not be able to do the same depending on your river’s location and how many other water features share the same name.
Plot your river to verify you have the correct one after you load in the geometry.
The code below loads the feature as a geodataframe (GeoPandas). So, if you want to use a digitized version from a local file you can just read that file in with gepandas and continue on with this tutorial.
You can check out this notebook for additional information on how to find your specific river feature.
river = ox.geocode_to_gdf('Snake River', which_result=1)
river = river.to_crs(dem.rio.crs)
river.plot()
<Axes: >
Crop the river geometry to the DEM extent¶
Your river geometry will probably cover a much larger area than the DEM you downloaded. Crop the river geometry to the DEM bounds to keep the analysis clean.
Plot the resulting geometry to verify that you have the correct river section.
river_cropped = river.clip(dem.rio.bounds())
xmin, ymin, xmax, ymax = river_cropped.bounds.iloc[0]['minx'], river_cropped.bounds.iloc[0]['miny'], river_cropped.bounds.iloc[0]['maxx'], river_cropped.bounds.iloc[0]['maxy']
bounds = box(xmin, ymin, xmax, ymax)
river_geom = river_cropped.geometry.iloc[0]
river_cropped.plot()
<Axes: >
Crop the DEM to the river bounding box¶
Now, it’s likely that your DEM covers non-riparian, non-valley-bottom areas. To simplify the analysis and reduce data size we can crop the DEM to the bounds of the river.
Note, because the river is a 1D shape, you may need to extend the bounds to capture the full area of interest. This will depend on the river’s orientation and width of your AOI around the river.
dem = dem.sel(y=slice(ymax, ymin), x=slice(xmin, xmax))
Plot the cropped DEM and the river¶
Plot the cropped DEM and overlay the river geometry to make sure you’re capturing the AOI as you expect.
Note: the DEM contains 3 dimensions, but only 1 band. This is just how rioxarray reads data to keep it consisent with multiband rasters. The squeeze method just makes dem 2-dimensional for easy plotting.
fig, ax = plt.subplots()
dem.squeeze().plot.imshow(ax=ax)
river_cropped.plot(ax=ax, color='red')
<Axes: title={'center': 'band = 1, spatial_ref = 0'}, xlabel='x', ylabel='y'>
4. Sample DEM values along the the river¶
At this point, your DEM and river should be lined up. Now we can sample the elevations from the DEM at points along the river. This will allow us to create a surface representing the channel/river elevation that will be a necessary, intermediate product for creating the REM.
Retrieve the X,Y coordinates of each vertex of the line representing the river. A better way to do this would be to segment the line into equal intervals (about channel width apart), but we’ll keep it simple and use the geometry as it is.
Create two data arrays. One to represent X-coordinates, and another for Y-coordinates.
xs, ys = river_geom.xy
xs, ys = xr.DataArray(xs, dims='z'), xr.DataArray(ys, dims='z')
Use the interp (interpolation) method to retrieve the elevation value nearest the point. This will give us a sample elevation for each vertex along the river.
sampled = dem.interp(x=xs, y=ys, method='nearest').dropna(dim='z')
sampled
<xarray.DataArray (band: 1, z: 45)>
array([[1993.74, 1994.64, 1994.78, 1994.92, 1995.47, 1995.9 , 1996.75,
1996.96, 1997.02, 1997.21, 1997.47, 1997.82, 1998.74, 1999.48,
2000.47, 2001.25, 2001.68, 2001.92, 2002.2 , 2002.79, 2003.31,
2004.02, 2004.32, 2004.61, 2005.67, 2005.8 , 2006.25, 2006.47,
2006.59, 2007.64, 2007.85, 2008.24, 2009.75, 2010.85, 2011.53,
2011.86, 2013.18, 2014.64, 2015.34, 2015.54, 2015.72, 2016.03,
2017.19, 2018.07, 2018.29]], dtype=float32)
Coordinates:
* band (band) int32 1
spatial_ref int32 0
x (z) float64 5.257e+05 5.259e+05 5.26e+05 ... 5.299e+05 5.3e+05
y (z) float64 4.84e+06 4.84e+06 4.84e+06 ... 4.845e+06 4.845e+06
Dimensions without coordinates: z
Attributes: (12/17)
AREA_OR_POINT: Area
DataType: Generic
ParentRasterType: Raster Dataset
LAYER_TYPE: athematic
STATISTICS_COVARIANCES: 5265.53043182074
STATISTICS_MAXIMUM: 2739.0200195313
... ...
STATISTICS_SKIPFACTORY: 1
STATISTICS_STDDEV: 72.563974752082
_FillValue: -3.4028235e+38
scale_factor: 1.0
add_offset: 0.0
long_name: Layer_15. Interpolate river elevations to the entire DEM grid¶
We’ll use the values sampled along the river to interpolate an associated river elevation for each pixel in the DEM grid.
The interpolated elevation represents the elevation of the stream channel locaiton nearest to each pixel in the raster. Basically, we’re associating each pixel with the nearest river channel elevation. When we calculate the REM this will make it so we can determine the height of each location above the river channel. That’s how the REM gets its name. It’s elevation relative to the river channel instead of relative to sea level.
To start, we need to relate the sampled values to nearby locations. There’s a lot going on here, but we’ll walk through it.
- arrange the coordinates of sampled locations in a 2D array (
c_sampled), where each row is a point, the first column is X values, and the second column is Y values - get lists of all X (
c_x) and Y (c_y) values from the DEM - create an array (
c_interpolate) defining the DEM grid (i.e., list every X,Y coordinate the occurs in the grid) - convert the sampled values (elevations) to a 1D array
This sets us up to do interpolation of river elevations to nearby locations.
c_sampled = np.vstack([sampled.coords[c].values for c in ('x', 'y')]).T
c_x, c_y = [dem.coords[c].values for c in ('x', 'y')]
c_interpolate = np.dstack(np.meshgrid(c_x, c_y)).reshape(-1, 2)
values = sampled.values.ravel()
To speed up the interpolation we’ll create an index (i.e., tree) so we can identify points nearest another point without iterating through every point each time a calculation is performed.
tree = KDTree(c_sampled) # index points to KD tree to easily find nearest neighbors
Now, do inverse distance weighted (IDW) interpolation. This is a mathematical method to fill in gaps that gives more weight to known values closer to unknown points. Here we’re calculating the elevation based on the 5 nearest points (k=5).
We’ll get the distance (and index) of a point’s five nearest neighbors (that’s the five nearest sampled points). Then we create weights that are inversely related to the distance. Next, divide the weight by the sum of all five neighbors. This gives a percentage/proportion that each point contributes to the final value. Now we just multiply the percentages/proportions by the associated sampeled elevation value and sum them up to get the interpolated elevation.
distances, indices = tree.query(c_interpolate, k=5)
weights = 1 / distances
weights = weights / weights.sum(axis=1).reshape(-1, 1)
interpolated_values = (weights * values[indices]).sum(axis=1)
This gives us an interpolated (estimated) river elevation for each pixel center in the DEM grid. Now we’ll convert the pixel centers to a 2D array so they can be displayed as a raster.
elevation_raster = xr.DataArray(
interpolated_values.reshape((len(c_y), len(c_x))).T, dims=('x', 'y'), coords={'x': c_x, 'y': c_y}
)
Plot the interpolated elevations with the river geometry to make sure everything turned out as expected.
fig, ax = plt.subplots()
elevation_raster.transpose().plot.imshow(ax=ax)
river_cropped.plot(ax=ax, color='red')
<Axes: xlabel='x', ylabel='y'>
6. Create the REM¶
It’s really easy to create the REM once we have an interpolated surface. We just subtract the interpolated surface (i.e., river elevation) from the original DEM. The result is the REM that gives us an estimate of each pixel’s height above the river.
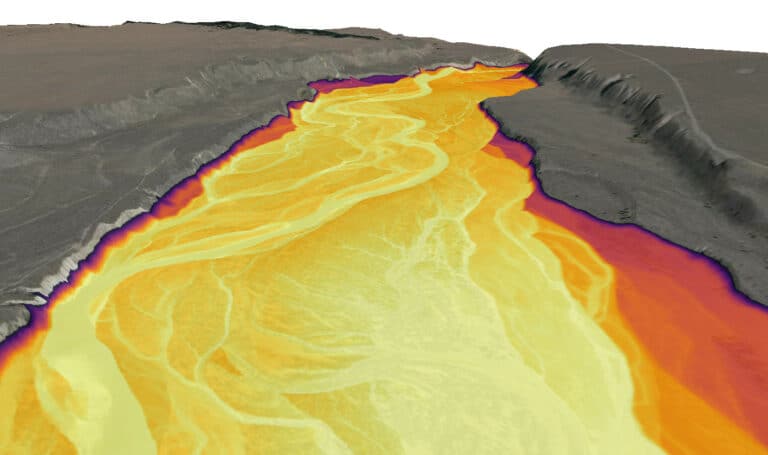
Calculate and plot the REM. You’ll notice that the downstream elevation gradient (i.e., slope) has been removed. We can easily see the valley bottom, terraces, and uplands.
rem = dem - elevation_raster
rem.plot()
<matplotlib.collections.QuadMesh at 0x169a3066f50>
7. Artistic visualization¶
To better see the river channel, side channels, and other surfaces in the valley-bottom — and make them pop like the examples you’ve seen — we need to adjust the visualization a little bit.
I’ll start by using this neat color visualization from DahnJ.
colors = ['#f2f7fb', '#81a8cb', '#37123d']
Next, limit the color map to elevations between 0 and 10 meters (span=[0, 10]). Essentially we only want to apply the gradient to surfaces 10 meters above the river channel. Everything else will be displayed as the end color on the map. This will give more contrast to features in the valley bottom. You may need to adjust the 0 and 10 values depending on your specific location.
You’ll notice some linear artifacts that are perpindicular to the river. These occur because the elevation sample points are spaced too far apart. Creating more sample points along the river will smooth out these artifacts. I demonstrate this in my QGIS tutorial on the same topic.
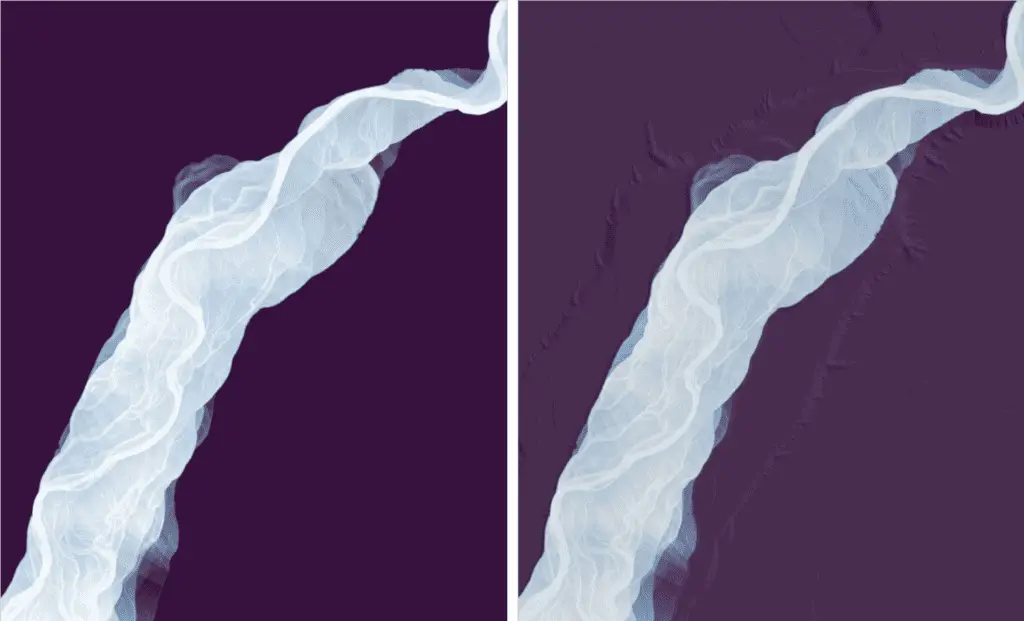
We can improve the visualization a little more by adding a hillshade and making the color map slighly transparent. This will allow the texture of land features to show through (second image).
Note: I added reindex(y=list(reversed(rem.y))) because datashader flipped the REM vertically. You can see from the image above that the REM is oriented correctly. For some reason, shade flipped it, so I flipped it back.
a = tf.shade(xrspatial.hillshade(dem.squeeze().reindex(y=list(reversed(dem.y))), angle_altitude=1, azimuth=310), cmap=['black', 'white'], how='linear')
b = tf.shade(rem.squeeze().reindex(y=list(reversed(rem.y))), cmap=colors, span=[0, 10], how='linear', alpha=200)
tf.Images(
tf.shade(rem.squeeze().reindex(y=list(reversed(rem.y))), cmap=colors, span=[0, 10], how='linear'),
tf.stack(a, b)
)
Heres the final result. Hillshade on the right.
Some things to consider
Remember the REM represents the height of locations above the river channel. One way to think about this is that it’s an estimate of how high the water would need to get to flood a specific location. Also, remember that we created this REM from an interpolation. This method is not adequate for actual flood analysis. Flood analysis methods have been developed from this concept but they involve additional lines of evidence such as river gage data and hydraulic model formulations.
Even without flood analysis, REMs create opportunities for really great river visualizations. They’re also very useful for analysis of geomorphic features because they remove the confounding effect of down-valley slope.
Hopefully, you’ll find fun ways to incorporate REMs into your daily work routines!